De stelling van Pythagoras
Te bewijzen: a2 + b2 = c2. Bewijs:
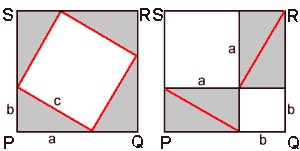
Opp. vierkant PQRS = c² + 4 grijze driehoeken.
Opp. vierkant PQRS = a² + b² + 4 grijze driehoeken
De grijze driehoeken zijn allemaal evengroot, namelijk rechthoekige driehoeken
met rechthoekszijden a en b, en schuine zijde c.
Gevolg: a² + b² = c²
Waarom is de vierhoek met zijde c in de linkerfiguur een vierkant?
Meer over de stelling van Pythagoras:
https://www.cut-the-knot.org/pythagoras/index.shtml#9
Pythagoras bij de Chinezen:
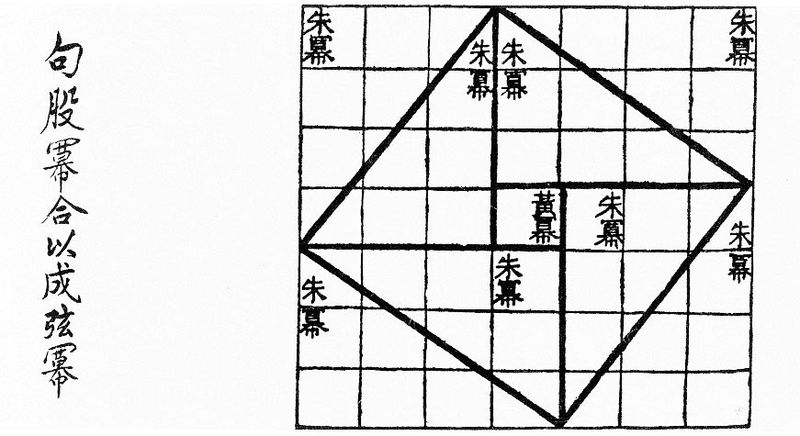
We zien hier met a=4, b=3 en c=5 uitgebeeld dat
(a+b)2 = c2 + 2ab en ook dat c2 = (a - b)2 + 2ab.
Beide gelijkheden zijn equivalent met c2 = a2 + b2.

We zien hier met a=4, b=3 en c=5 uitgebeeld dat
(a+b)2 = c2 + 2ab en ook dat c2 = (a - b)2 + 2ab.
Beide gelijkheden zijn equivalent met c2 = a2 + b2.